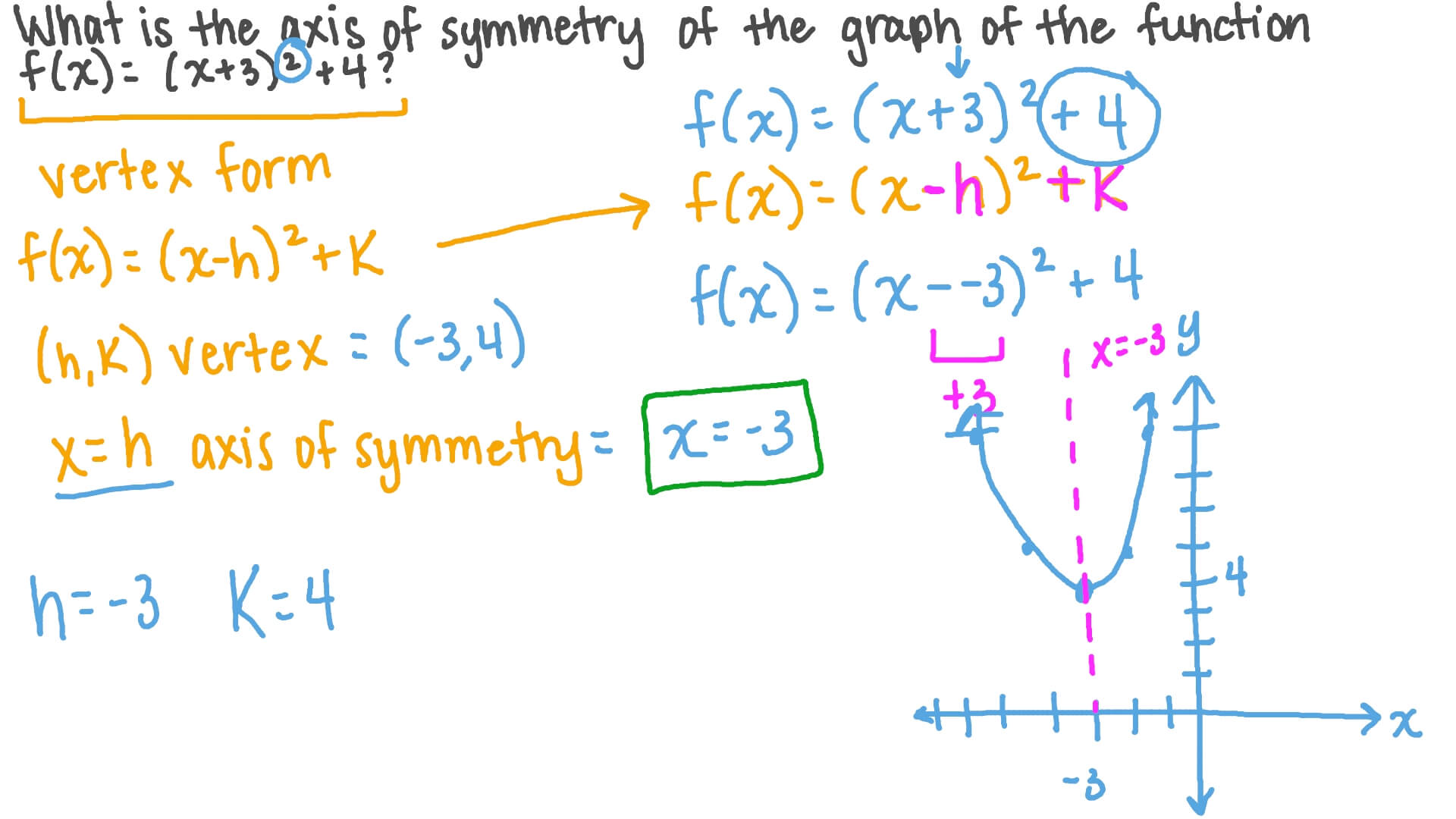The world of mathematics is filled with fascinating concepts that challenge our understanding and expand our knowledge. One such concept is the "line of symmetry equation," which is integral to geometry and helps us understand the balance and proportion of various shapes and figures. This equation plays a crucial role in determining symmetry, an essential property that contributes to the aesthetic appeal of objects and structures in both natural and man-made environments.
In geometry, symmetry refers to a situation where a shape or figure can be divided into two identical halves. The dividing line is known as the line of symmetry. The line of symmetry equation allows us to mathematically represent this line, enabling precise calculations and analyses. It's a concept that bridges the gap between abstract mathematical theories and their practical applications in the real world. Understanding this equation is vital for anyone interested in geometry, architecture, or any field where symmetry is essential.
This article aims to provide a comprehensive exploration of the line of symmetry equation, delving into its significance, derivation, and applications. We'll cover its relevance in various mathematical contexts, explore its applications in different fields, and answer some frequently asked questions. Whether you're a student, a teacher, or a professional, this guide will help you master the line of symmetry equation, ensuring a solid understanding of its principles and uses.
Read also:Insights Into Charles Meltons Wife And Their Relationship
Table of Contents
- What is the Line of Symmetry Equation?
- Historical Perspective
- Importance in Mathematics
- Deriving the Line of Symmetry Equation
- Applications in Geometry
- Real-World Applications
- How Does it Relate to Other Mathematical Concepts?
- Common Misconceptions
- Line of Symmetry Equation in Education
- Advanced Applications and Research
- How Does it Enhance Architectural Designs?
- Using Technology to Master the Concept
- What Role Does it Play in Visual Arts?
- Frequently Asked Questions
- Conclusion
What is the Line of Symmetry Equation?
The line of symmetry equation is a mathematical expression that defines the line dividing a figure into two mirror-image halves. In its simplest form, this line can be represented as a vertical or horizontal line when dealing with basic geometric shapes like squares and rectangles. However, when applied to more complex figures, the equation may involve more advanced algebraic expressions.
For a parabola, which is a common curve in mathematics, the line of symmetry is vertical and can be expressed as x = -b/2a where 'a' and 'b' are coefficients from the quadratic equation ax² + bx + c = 0. This particular equation is crucial in graphing parabolas and finding their vertex, allowing for a deeper understanding of their properties.
Symmetry lines are not only limited to straight lines but can also be curved, depending on the shape in question. In circles, any line that passes through the center acts as a line of symmetry. Similarly, for regular polygons, the number of symmetry lines corresponds to the number of sides, each bisecting the shapes into congruent parts.
Historical Perspective
The concept of symmetry has been a cornerstone of mathematics since ancient times. Early civilizations such as the Greeks and Egyptians recognized the aesthetic and practical value of symmetry, applying it in architecture and art. The mathematical exploration of symmetry can be traced back to Euclid's "Elements," where he systematically studied geometric figures and their properties.
Over the centuries, mathematicians have expanded upon these early ideas, formalizing the principles of symmetry and developing equations to describe them. The line of symmetry equation emerged as a tool for analyzing geometric shapes, enabling mathematicians to quantify symmetry and apply it to various mathematical and real-world problems.
The Renaissance period brought a renewed interest in symmetry, with artists and architects incorporating mathematical principles into their work. This era marked a significant advancement in the understanding of symmetry, leading to more sophisticated equations and applications.
Read also:The Timeless Appeal Of Musician Joe Walsh A Look At His Age And Life
Importance in Mathematics
Symmetry is a fundamental concept in mathematics, and the line of symmetry equation is essential for its study. This equation allows mathematicians to identify symmetry in geometric figures, providing a basis for understanding their properties and behavior. Symmetry is not only a theoretical concept but also has practical applications in fields such as physics, engineering, and computer science.
In mathematics, symmetry is often associated with balance and harmony, making it a key component in solving problems related to geometry, algebra, and calculus. The line of symmetry equation provides a framework for analyzing these problems, enabling mathematicians to develop solutions and make predictions.
Moreover, the study of symmetry extends beyond simple geometric shapes, encompassing complex structures and patterns found in nature. The line of symmetry equation is instrumental in exploring these patterns, allowing mathematicians to uncover the underlying principles that govern their formation.
Deriving the Line of Symmetry Equation
Deriving the line of symmetry equation involves understanding the properties of the geometric figure in question. For simple shapes like squares and rectangles, the line of symmetry is often a straightforward vertical or horizontal line. However, for more complex figures, the derivation may require advanced mathematical techniques.
For parabolas, the line of symmetry equation is derived from the quadratic equation ax² + bx + c = 0. By completing the square or using calculus, mathematicians can find the vertex of the parabola, which lies on the line of symmetry. The equation for the line of symmetry is then given by x = -b/2a, providing a precise mathematical description of the line.
In the case of circles, the line of symmetry is any line that passes through the center, as all points equidistant from the center form a symmetrical shape. For regular polygons, the symmetry lines are derived by bisecting the angles between the vertices, resulting in a set of congruent triangles that demonstrate the shape's symmetry.
Applications in Geometry
The line of symmetry equation is a powerful tool in geometry, used to analyze and understand the properties of various shapes and figures. It enables the identification of symmetrical features, providing insight into the balance and proportion of geometric objects.
In geometry, the line of symmetry equation is applied to a wide range of shapes, from simple polygons to complex curves. By identifying the line of symmetry, mathematicians can simplify calculations, make accurate predictions, and solve problems more efficiently.
Furthermore, the line of symmetry equation is used in the construction and design of geometric models, allowing for the creation of symmetrical structures that are both aesthetically pleasing and structurally sound. This application is particularly relevant in fields such as architecture and engineering, where symmetry is often a key consideration.
Real-World Applications
The line of symmetry equation has numerous real-world applications, extending beyond the realm of mathematics to various fields such as physics, biology, and art. In physics, symmetry plays a crucial role in understanding the laws of nature, with the line of symmetry equation providing a mathematical framework for analyzing symmetrical phenomena.
In biology, symmetry is a common feature in the structure of living organisms, from the bilateral symmetry of animals to the radial symmetry of flowers. The line of symmetry equation helps biologists understand these patterns, offering insight into the evolutionary processes that shape life on Earth.
In art and design, symmetry is often used to create visually appealing compositions. The line of symmetry equation allows artists and designers to achieve balance and harmony in their work, enhancing the aesthetic impact of their creations.
How Does it Relate to Other Mathematical Concepts?
The line of symmetry equation is closely related to several other mathematical concepts, including transformations, congruence, and tessellations. Understanding these relationships is essential for a comprehensive understanding of geometry and its applications.
Transformations, such as reflections, rotations, and translations, are often used in conjunction with the line of symmetry equation to manipulate geometric figures. These transformations preserve symmetry, allowing mathematicians to explore the properties of shapes in different orientations and positions.
Congruence is another important concept related to symmetry, as it involves the comparison of geometric figures based on their size and shape. The line of symmetry equation helps identify congruent parts of a figure, enabling the analysis of their similarities and differences.
Tessellations, or the tiling of a plane with geometric shapes, also rely on symmetry. The line of symmetry equation is used to create repeating patterns, ensuring that the shapes fit together seamlessly without gaps or overlaps.
Common Misconceptions
There are several misconceptions associated with the line of symmetry equation, often stemming from a lack of understanding of the underlying principles. One common misconception is that all shapes have a line of symmetry, which is not the case. Many shapes, such as scalene triangles and irregular polygons, do not possess any symmetrical lines.
Another misconception is that the line of symmetry is always a straight line. While this is true for most basic geometric shapes, some figures, like certain curves and designs, may have curved lines of symmetry.
Additionally, some people mistakenly believe that the line of symmetry equation is only applicable to two-dimensional shapes. In reality, the concept of symmetry extends to three-dimensional objects, with lines of symmetry being replaced by planes of symmetry.
Line of Symmetry Equation in Education
The line of symmetry equation is an important topic in mathematics education, providing students with a foundation for understanding symmetry and its applications. Teaching this concept helps students develop critical thinking and problem-solving skills, as they learn to analyze geometric figures and identify symmetrical features.
In the classroom, educators use a variety of methods to teach the line of symmetry equation, including visual aids, interactive activities, and hands-on experiments. These approaches help students grasp the concept more effectively, making learning engaging and enjoyable.
Moreover, the line of symmetry equation serves as a stepping stone to more advanced mathematical topics, such as transformations and congruence. By mastering this concept, students are better prepared to tackle complex problems and explore the fascinating world of geometry.
Advanced Applications and Research
In recent years, advanced applications and research have expanded the understanding and use of the line of symmetry equation. Mathematicians and scientists are exploring new ways to apply this concept in various fields, from robotics to nanotechnology.
In robotics, symmetry is crucial for designing stable and efficient machines. The line of symmetry equation is used to create symmetrical designs that enhance the performance and functionality of robotic systems.
In nanotechnology, researchers are investigating the role of symmetry in the behavior of nanomaterials. The line of symmetry equation helps predict the properties of these materials, paving the way for innovations in fields such as medicine and electronics.
How Does it Enhance Architectural Designs?
Symmetry is a fundamental principle in architectural design, contributing to the aesthetic appeal and structural integrity of buildings. The line of symmetry equation plays a key role in achieving these objectives, guiding architects in the creation of balanced and harmonious structures.
Architects use the line of symmetry equation to design buildings that are both functional and visually striking. By incorporating symmetrical elements, they create spaces that are pleasing to the eye and comfortable to inhabit.
Furthermore, the line of symmetry equation helps architects ensure the stability of their designs, as symmetrical structures are often more resilient to external forces. This application is particularly important in the construction of bridges, towers, and other large-scale projects.
Using Technology to Master the Concept
Technology has revolutionized the way we learn and apply mathematical concepts, including the line of symmetry equation. With the advent of digital tools and resources, students and professionals can explore symmetry in new and innovative ways.
Software programs and applications provide interactive platforms for studying the line of symmetry equation, allowing users to manipulate geometric figures and observe the effects of symmetry in real-time. These tools enhance the learning experience, making it more engaging and accessible.
Moreover, technology enables the visualization of complex symmetrical patterns that would be difficult to analyze using traditional methods. This capability is particularly valuable in fields such as design and engineering, where precision and accuracy are paramount.
What Role Does it Play in Visual Arts?
Symmetry is a powerful tool in the visual arts, used to create compositions that are both balanced and dynamic. The line of symmetry equation helps artists achieve these effects, guiding them in the arrangement of shapes and forms.
In painting and sculpture, symmetry is often employed to evoke a sense of harmony and order. The line of symmetry equation provides a mathematical basis for this artistic principle, enabling artists to create works that resonate with viewers on a deeper level.
Additionally, the line of symmetry equation plays a role in the design of decorative patterns and motifs. By understanding the principles of symmetry, artists can develop intricate designs that captivate the eye and inspire the imagination.
Frequently Asked Questions
1. What is the line of symmetry in a parabola?
The line of symmetry in a parabola is a vertical line that passes through its vertex. It can be represented by the equation x = -b/2a, where 'a' and 'b' are coefficients of the quadratic equation ax² + bx + c = 0.
2. Can all shapes have a line of symmetry?
No, not all shapes have a line of symmetry. For example, scalene triangles and irregular polygons do not possess symmetrical lines. Symmetry is a property that some shapes have, but not all.
3. How is the line of symmetry equation used in real-world applications?
The line of symmetry equation is used in various real-world applications, including architecture, art, biology, and physics. It helps in designing balanced structures, understanding patterns in nature, and creating aesthetically pleasing compositions.
4. Is the line of symmetry always a straight line?
While the line of symmetry is often a straight line for simple shapes, some complex figures may have curved lines of symmetry. It depends on the geometry of the shape in question.
5. How does symmetry relate to transformations?
Symmetry is closely related to transformations such as reflections, rotations, and translations. These transformations preserve symmetry, allowing mathematicians to explore the properties of shapes in different orientations.
6. What is the role of technology in understanding the line of symmetry equation?
Technology provides tools and resources that enhance the understanding of the line of symmetry equation. Software programs and applications offer interactive platforms for studying symmetry, enabling users to visualize and manipulate geometric figures effectively.
Conclusion
The line of symmetry equation is a fundamental concept in mathematics, offering insight into the principles of symmetry and its applications. By understanding this equation, students and professionals can explore the fascinating world of geometry, uncovering the beauty and complexity of symmetrical patterns and structures.
From its historical origins to its modern applications, the line of symmetry equation remains a vital tool for mathematicians, scientists, and artists alike. Its significance extends beyond theoretical mathematics, influencing various fields and contributing to advancements in technology, design, and art.
As we continue to explore the possibilities of the line of symmetry equation, we open the door to new discoveries and innovations, enriching our understanding of the world around us and inspiring future generations to pursue the study of symmetry and its many wonders.